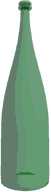
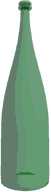
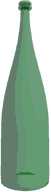
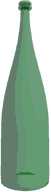The Average Bottle Fallacy What is the average energy content of the wind at your wind turbine site? Most people who are new to wind energy think they could easily live without the Weibull distribution. After all, if we know the average wind speed, we also know the average power of the wind, don't we? So, can't we just use the power (or energy) at the mean wind speed to figure out how much power (or energy) will hit the wind turbine? In other words, couldn't we just say, that with an average wind speed of 7 m/s we get an average power input of 210 Watts per square metre of rotor area? (You may find that figure in the table on the power of the wind in the Reference Manual). The answer is no! We would underestimate wind resources by almost 100 per cent. If we did that, we would be victims of what we could call the Average Bottle Fallacy: Look at the smallest and largest bottle in the picture. Both have exactly the same shape. One is 0.24 m tall, the other is 0.76 m tall. How tall is the average bottle? If you answer 0.5 m tall, you are a victim of the Average Bottle Fallacy. Bottles are interesting because of their volume, of course. But the volume varies with the cube (the third power) of their size. So, even though the largest bottle is only 3.17 times larger than the small bottle, its volume is actually 3.173=32 times larger than the small bottle. The average volume is therefore 16.5 times that of the small bottle. This means that a bottle with an average volume would have to be 2.55 times the height of the small bottle, i.e. 0.61 m tall. (Since 2.553 = 16.5). The point we are trying to make, is that you cannot simply take an average of wind speeds, and then use the average wind speed for your power calculations. You have to weigh each wind speed probability with the corresponding amount of power. On the next two pages we shall calculate the energy in the wind. First we use the bottle example to grasp the idea, then we use simple math.
	| Back | Home | Forward | © Copyright 1998 Soren Krohn. All rights reserved. Updated 6 August 2000 http://www.windpower.org/tour/wares/bottle.htm