Proof of Betz' Law

This page gives a proof of Betz' law. Before reading this page you should have read the pages in the Guided Tour on how the wind turbine deflects the wind and Betz' Law. If you do not follow the argument in detail, just glance through the rest of this page, which uses Betz' own reasoning from his book Wind-Energie from 1926 to explain the law.

Proof of Betz' Theorem
Let us make the reasonable assumption that the average wind speed through the rotor area is the average of the undisturbed wind speed before the wind turbine, v₁, and the wind speed after the passage through the rotor plane, v₂, i.e. (v₁+v₂)/2. (Betz offers a proof of this).
The mass of the air streaming through the rotor during one second is

m =  F (v₁+v₂)/2

where m is the mass per second, is the density of air, F is the swept rotor area and [(v₁+v₂)/2] is the average wind speed through the rotor area. The power extracted from the wind by the rotor is equal to the mass times the drop in the wind speed squared (according to Newton's second law):

Substituting m into this expression from the first equation we get the following expression for the power extracted from the wind:

P = (/4) (v₁² - v₂²) (v₁+v₂) F

Now, let us compare our result with the total power in the undisturbed wind streaming through exactly the same area F, with no rotor blocking the wind. We call this power P₀:

P₀ = (/2) v₁³ F

The ratio between the power we extract from the wind and the power in the undisturbed wind is then:

We may plot P/P₀ as a function of v₂/v₁:

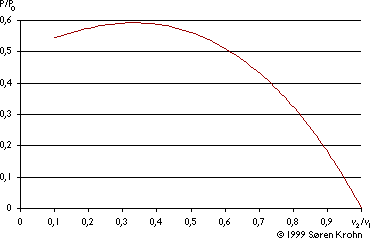
We can see that the function reaches its maximum for v₂/v₁ = 1/3, and that the maximum value for the power extracted from the wind is 0,59 or 16/27 of the total power in the wind.

Click here to go back the Guided Tour page on Betz' Law.